10 Centralidad
La centralidad es uno de los conceptos más antiguos del ARSo. Un actor central puede ser alguien que tiene numerosos vínculos con otros actores (grado), alguien que está más cerca (en términos de distancia del camino) a todos los demás (cercanía), alguien que se encuentra en el camino más corto (geodésico) entre dos actores cualesquiera (intermediación), o alguien que tiene vínculos con otros actores muy centrales (eigenvector). En algunas redes, los mismos actores obtienen una puntuación alta en las cuatro medidas, en otras no.
Por supuesto, hay más de cuatro medidas de centralidad. UCINET implementa más de 20, el programa R CINNA incluye más de 40, y David Schoch ha creado una tabla periódica interactiva de más de 100 medidas de centralidad.
Aquí discutiremos las tres centralidades más comunes, originalmente desarrolladas por Freeman (1979), es decir: grado, cercanía e intermediación. Además, otras medidas importantes serán introducidas como eigenvector (Bonacich, 1987), grados de entrada y salida (Wasserman & Faust, 1994) y centros de actividad y autoridades (Kleinberg, 1999). Para diferenciar entre medidas destinadas para datos dirigidos y no-dirigidos, dividiremos el capítulo en dos secciones. Adicionalmente, utilizaremos el marco teórico, originalmente postulado por Freeman (1979), utilizado en Cunningham, Everton, & Murphy (2016) para clasificar las medidas de centralidad en tres familias: medidas basadas en frecuencia, medidas basadas en distancia y medidas basadas en caminos. Como en todos los capítulos, este concluirá con un ejercicio práctico en Gephi.
10.1 Datos No Dirigidos: Centralidad y Poder
Aquí consideramos algunas de las medidas de centralidad apropiadas para trabajar con datos no dirigidos. Para clarificar algunas de las similitudes y diferencias entre estas medidas, serán presentadas utilizando el sistema de clasificación en Cunningham, Everton, & Murphy (2016). Específicamente, en tres secciones:
- Basadas en frecuencia: la característica unificadora de estas es el enfoque en la frecuencia con la que un actor tiene vínculos con otros en la red. Por ello, estas suponen que la alta frecuencia de enlaces es correspondiente a poder o importancia en la red.
- Basadas en distancia: estas asumen que las distancias entre actores es el factor principal en determinar la centralidad y poder de cada nodo.
- Basadas en caminos: estas se basan en la ubicación de un nodo en la red, principalmente si esta ubicación es una posición de corretaje o intermediación.
10.1.1 Medidas Basadas en Frecuencia
10.1.1.1 Centralidad de Grado
La centralidad de grado es la medida más simple y fácil de calcular y entender, por ello comisaremos aquí. Esta medida se define como el conteo de vínculos de un actor. En una red no dirigida, no tomamos en cuenta si estos enlaces son “de” o “hacia” el nodo. Con esto en mente, para una red binaria la centralidad de grado se define formalmente como:
\[ C_i^{deg} = \sum\limits_{j=1}^n x_{ij} \] Donde la medida se calcula para todos los nodos en un grafo. Es decir, el grado se define como la suma de los vínculos entre un nodo (\(i\)) hacia actores adyacentes (\(x_{ij}\)). Por ejemplo, el grado de centralidad de los nodos en la Figura 10.1 aparecen en la Tabla 10.1. El nodo con mayor grado en este grafo es A puesto a que se encuentra enlazado con cuatro otros, D y E tienen un grado de centralidad de dos y finalmente C y B tienen un grado de uno.
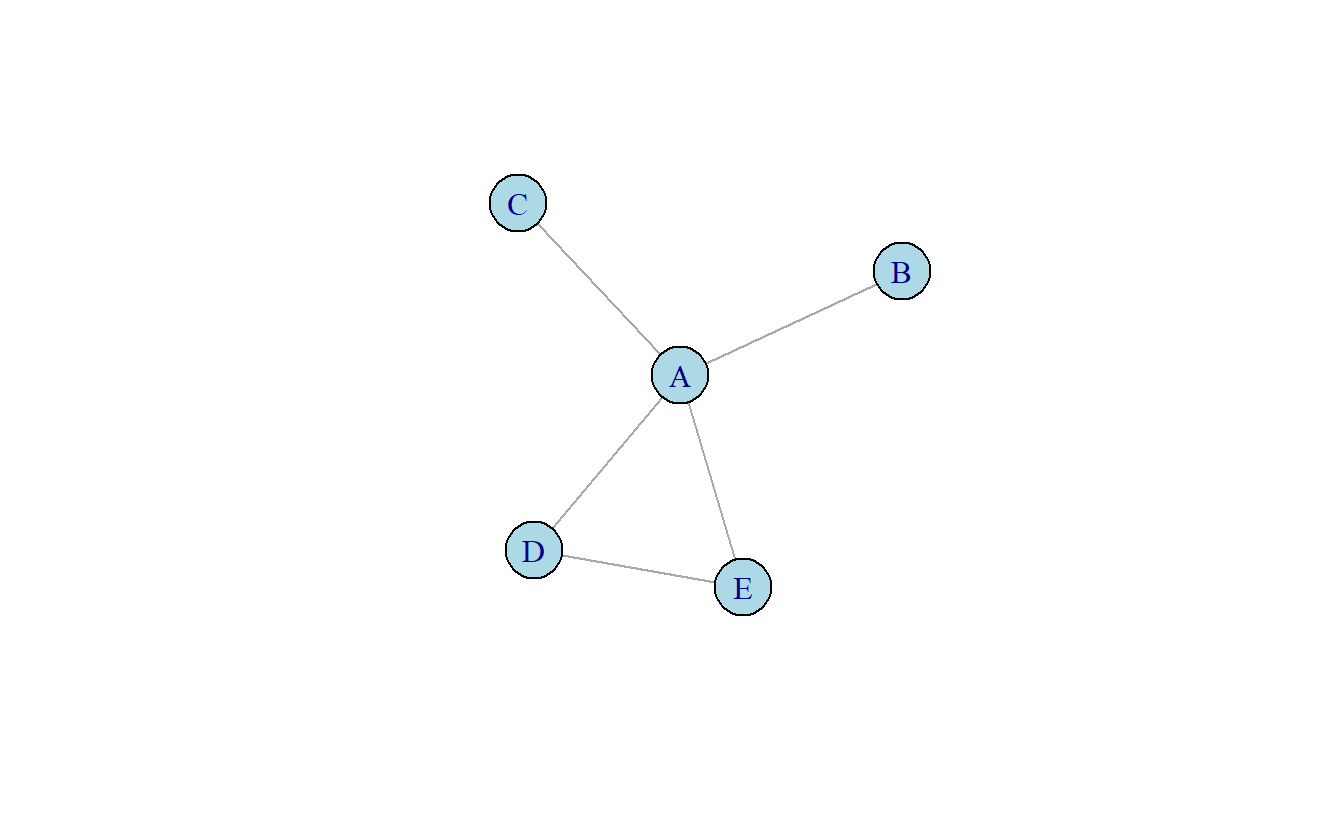
Figura 10.1: Grafo no dirigido
| Nombre | Grado |
|---|---|
| A | 4 |
| B | 1 |
| C | 1 |
| D | 2 |
| E | 2 |
Existen múltiples maneras de calcular esta medida de manera programática. Sin embargo, el método más simple es multiplicar la matriz de adyacencia por un vector de unos, donde el largo del vector es correspondiente a el número de vértices en el grafo (Meghanathan, 2016). La siguiente operación ilustra como computar dicho índice.
\[ \begin{matrix} & A & B & C & D & E \\ A & 0 & 1 & 1 & 1 & 1 \\ B & 1 & 0 & 0 & 0 & 0 \\ C & 1 & 0 & 0 & 0 & 0 \\ D & 1 & 0 & 0 & 0 & 1 \\ E & 1 & 0 & 0 & 1 & 0 \end{matrix} \enspace\times\enspace \begin{matrix} \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{matrix} \enspace=\enspace \begin{matrix} & C_i^{deg} \\ A & 4 \\ B & 1 \\ C & 1 \\ D & 2 \\ E & 2 \end{matrix} \tag{10.1} \]
Como todas las medidas en esta sección, la manera en la que se calcula el grado de centralidad es indicativo del objetivo de la medida y como se debe interpretar. Cunningham, Everton, & Murphy (2016) postulan que el grado mide la popularidad de un actor en términos de influencia directa entre este y otros nodos directamente adyacentes (Cunningham, Everton, & Murphy, 2016, p. 147). La idea principal aquí es que los vínculos sirven como canales para el flujo de influencia, materiales, ideas, etc. Por consiguiente, un nodo como A en la Figura 10.1 que ha invertido su tiempo y recursos en enlazarse con cuatro otros nodos en una red, es posiblemente más activo en la red que un actor como B conexo solo a un nodo.
Similarmente, los nodos con alto grado de centralidad tienden a ser más visibles en la red. Si asumimos que ciertos bienes – por ejemplo, información – tienden a difundirse en una red por medio de los enlaces, entonces podemos asumir que aquellos nodos con alto grado de centralidad estarán bien informados (Borgatti, Everett, & Johnson, 2018). Por ejemplo, en la Figura 10.1 el nodo A puede recibir información de tres ubicaciones aisladas, de los nodos B o C, y de la tríada compuesta con D y E. En contraste, B y C solo pueden acceder a información de la red a través de A. Similarmente, D y B dependen de A para acceder a recursos no redundantes en la tríada.
10.1.1.2 Centralidad de Eigenvector
La centralidad de eigenvector, o centralidad de auto vector (“eigen” significa “propio”), puede ser descrita de múltiples maneras. Aquí la categorizamos como una medida basada en frecuencia de vínculos similar a la centralidad de grado, pero con una variación clave, en esta medida ponderamos el grado de cada nodo por la centralidad de los nodos adyacentes (Borgatti, Everett, & Johnson, 2018). Esta medida asume que los enlaces a actores altamente centrales son más importantes que los enlaces a nodos en la periferia (Cunningham, Everton, & Murphy, 2016). En otras palabras, es preferible tener conexiones a nodos bien conectados. Por ejemplo, en la Figura 10.2 los nodos A y F tienen la misma centralidad de grado (2). Sin embargo, A se encuentra conectado a nodos quienes a su vez tienen un numero de enlaces limitado. En contraste, F se encuentra conectado a G y H los cuales son adyacentes a tres otros nodos. En este ejemplo, si el analista enfoca su análisis en centralidad de grado, que mide actividad directa, A y F son equivalentes. Sin embargo, si expandimos el enfoque del análisis para considerar la influencia indirecta, es aparente que F se encuentra en una posición superior al nodo A en base al alcance de sus conexiones indirectas.
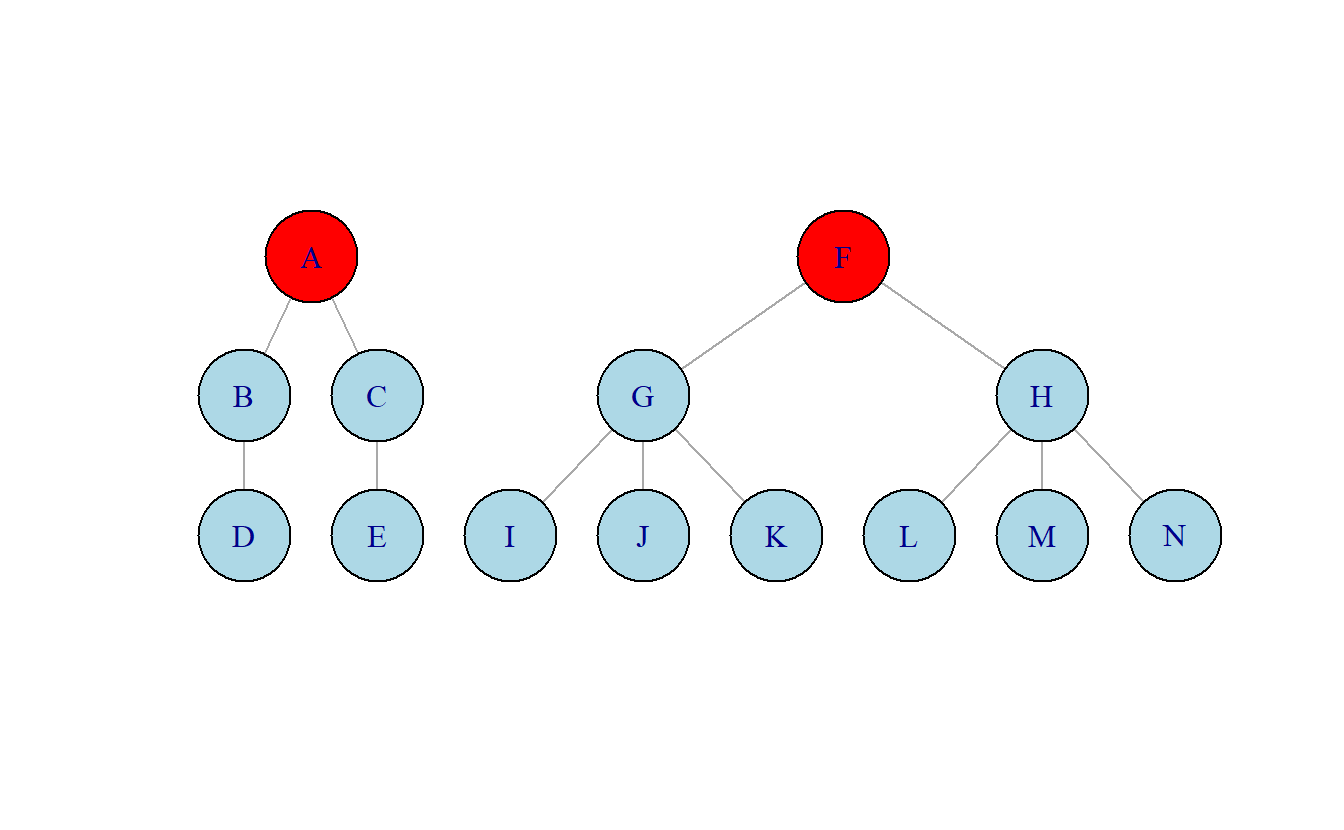
Figura 10.2: Comparación de nodos (A y F) con el mismo grado
De manera formal, Bonacich (1987) postula que la centralidad de eigenvector para cada nodo (\(i\)) corresponde a:
\[ e_i = \frac{1}{\lambda} \sum_j R_{ij}e_j \]
Donde \(R\) corresponde a la matriz de adyacencia, la cual es usualmente (pero no obligatoriamente) simétrica y los elementos de la diagonal son iguales a cero. Además, \(\lambda\) es la constante llamada eigenvalor requerido. Por convención, el eigenvalor más grande es preferido. Para determinar el eigenvalor principal de una red podemos emplear una serie de herramientas de software (Gephi calcula este valor en segundos) o el método de las potencias (Meghanathan, 2016). Las siguientes operaciones representan el proceso de calcular la centralidad de eigenvector para el gráfico en la Figura 10.3.
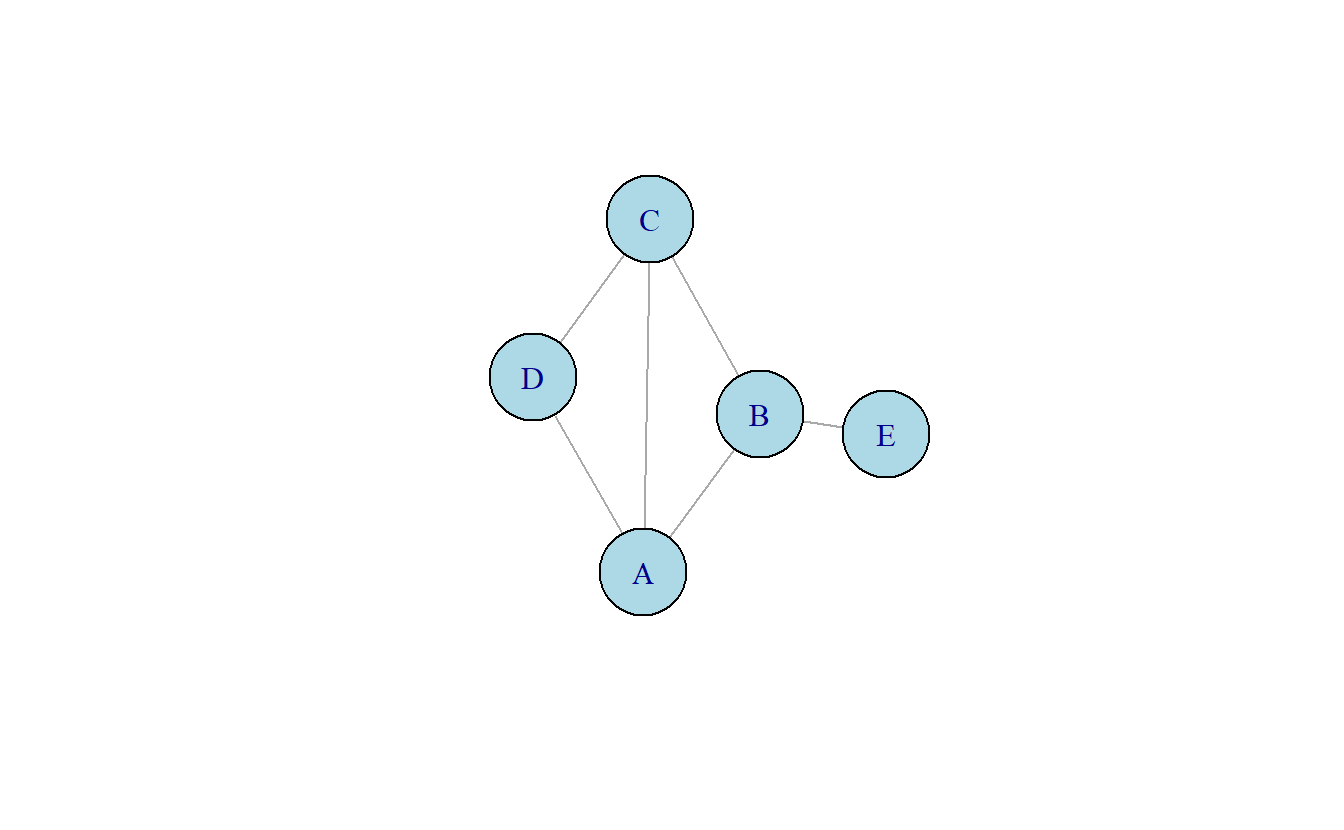
Figura 10.3: Grafo no dirigido
\[ \begin{split} Primera\ Iteración: \\& \begin{matrix} & A & B & C & D & E \\ A & 0 & 1 & 1 & 1 & 0 \\ B & 1 & 0 & 1 & 0 & 1 \\ C & 1 & 1 & 0 & 1 & 0 \\ D & 1 & 0 & 1 & 0 & 0 \\ E & 0 & 1 & 0 & 0 & 0 \\ \end{matrix} \quad \times \quad \begin{matrix} \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{matrix} \enspace=\enspace \begin{matrix} \\ 3 \\ 3 \\ 3 \\ 2 \\ 1 \end{matrix} \equiv \begin{matrix} \\ 0.5303\\ 0.5303 \\ 0.5303 \\ 0.3535 \\ 0.1768 \end{matrix}\\ &Vector\ normalizado = 5.6569 \end{split} \]
\[ \begin{split} Segunda\ Iteración:\\& \begin{matrix} & A & B & C & D & E \\ A & 0 & 1 & 1 & 1 & 0 \\ B & 1 & 0 & 1 & 0 & 1 \\ C & 1 & 1 & 0 & 1 & 0 \\ D & 1 & 0 & 1 & 0 & 0 \\ E & 0 & 1 & 0 & 0 & 0 \\ \end{matrix} \quad \times \quad \begin{matrix} \\ 0.5303\\ 0.5303 \\ 0.5303 \\ 0.3535 \\ 0.1768 \end{matrix} \enspace=\enspace \begin{matrix} \\ 1.4142 \\ 1.2374 \\ 1.4142 \\ 1.0606 \\ 0.5303 \end{matrix} \equiv \begin{matrix} \\ 0.6365 \\ 0.5569 \\ 0.6365 \\ 0.4773 \\ 0.2387 \end{matrix} \\ &Vector\ normalizado = 2.221984 \end{split} \]
\[ \begin{split} Tercera\ Iteración: \\& \begin{matrix} & A & B & C & D & E \\ A & 0 & 1 & 1 & 1 & 0 \\ B & 1 & 0 & 1 & 0 & 1 \\ C & 1 & 1 & 0 & 1 & 0 \\ D & 1 & 0 & 1 & 0 & 0 \\ E & 0 & 1 & 0 & 0 & 0 \\ \end{matrix} \quad \times \quad \begin{matrix} \\ 0.6365 \\ 0.5569 \\ 0.6365 \\ 0.4773 \\ 0.2387 \end{matrix} \enspace=\enspace \begin{matrix} \\ 1.6707 \\ 1.5117 \\ 1.6707 \\ 1.273 \\ 0.5569 \end{matrix} \equiv \begin{matrix} \\ 0.5337 \\ 0.4829 \\ 0.5337 \\ 0.4067 \\ 0.1779 \end{matrix} \\ &Vector\ normalizado = 3.130236 \end{split} \]
\[ \begin{split} Cuarta\ Iteración: \\& \begin{matrix} & A & B & C & D & E \\ A & 0 & 1 & 1 & 1 & 0 \\ B & 1 & 0 & 1 & 0 & 1 \\ C & 1 & 1 & 0 & 1 & 0 \\ D & 1 & 0 & 1 & 0 & 0 \\ E & 0 & 1 & 0 & 0 & 0 \\ \end{matrix} \quad \times \quad \begin{matrix} \\ 0.5337 \\ 0.4829 \\ 0.5337 \\ 0.4067 \\ 0.1779 \end{matrix} \enspace=\enspace \begin{matrix} \\ 1.4233 \\ 1.2454 \\ 1.4233 \\ 1.0675 \\ 0.4829 \end{matrix} \equiv \begin{matrix} \\ 0.5389 \\ 0.4715 \\ 0.5389 \\ 0.4041 \\ 0.1828 \end{matrix} \\ &Vector\ normalizado = 2.641108 \end{split} \]
\[ \begin{split} Quinta\ Iteración: \\& \begin{matrix} & A & B & C & D & E \\ A & 0 & 1 & 1 & 1 & 0 \\ B & 1 & 0 & 1 & 0 & 1 \\ C & 1 & 1 & 0 & 1 & 0 \\ D & 1 & 0 & 1 & 0 & 0 \\ E & 0 & 1 & 0 & 0 & 0 \\ \end{matrix} \quad \times \quad \begin{matrix} \\ 0.5389 \\ 0.4715 \\ 0.5389 \\ 0.4041 \\ 0.1828 \end{matrix} \enspace=\enspace \begin{matrix} \\ 1.4146 \\ 1.2607 \\ 1.4146 \\ 1.0778 \\ 0.4715 \end{matrix} \equiv \begin{matrix} \\ 0.5356 \\ 0.4773 \\ 0.5356 \\ 0.4081 \\ 0.1785 \end{matrix} \\ &Vector\ normalizado = 2.641162 \end{split} \]
\[ \begin{split} Sexta\ Iteración: \\& \begin{matrix} & A & B & C & D & E \\ A & 0 & 1 & 1 & 1 & 0 \\ B & 1 & 0 & 1 & 0 & 1 \\ C & 1 & 1 & 0 & 1 & 0 \\ D & 1 & 0 & 1 & 0 & 0 \\ E & 0 & 1 & 0 & 0 & 0 \\ \end{matrix} \quad \times \quad \begin{matrix} \\ 0.5356 \\ 0.4773 \\ 0.5356 \\ 0.4081 \\ 0.1785 \end{matrix} \enspace=\enspace \begin{matrix} \\ 1.4210 \\ 1.2497 \\ 1.4210 \\ 1.0712 \\ 0.4773 \end{matrix} \equiv \begin{matrix} \\ 0.5380 \\ 0.4731 \\ 0.5380 \\ 0.4055 \\ 0.1807 \end{matrix} \\ &Vector\ normalizado = 2.641176 \end{split} \] \[ ... \] \[ \begin{split} Decimonovena\ Iteración: \\& \begin{matrix} Nodo & A & B & C & D & E \\ Eigenvector & 0.537 & 0.475 & 0.537 & 0.407 & 0.179 \end{matrix} \\ &Vector\ normalizado = 2.641186 \\ \end{split} \tag{10.2} \]
Como puede ver, el método de las potencias es un proceso iterativo. Comienza al multiplicar la matriz por un vector con valores de uno, el cual produce el grado de centralidad. Normalizamos los valores de dicho vector, en la primera ronda 5.6569, y dividimos el producto de la multiplicación de matriz por el valor normalizado, esto produce un eigenvector tentativo. La siguiente ronda comienza multiplicando la matriz de adyacencia por el eigenvector tentativo de la ronda previa. Una vez más normalizamos el vector resultante de la multiplicación y dividimos dichos valores por el valor normalizado. Esencialmente este proceso continua hasta que el producto de la normalización del vector converge (Meghanathan, 2016). En el ejemplo previo, este proceso toma 19 iteraciones para concluir. Sin embargo, alrededor de la cuarta iteración empezamos a ver un valor similar a el valor convergente de en la última y penúltima ronda.
Después de tanta aritmética, se ha de estar preguntando ¿cómo interpreto los índices de centralidad resultantes? Como se mencionó previamente, esta medida de centralidad toma en cuenta los enlaces de cada nodo, así como los enlaces de sus vecinos. En términos prácticos el software habitualmente genera una serie de valores donde los índices más grandes representan nodos con mayor influencia indirecta. Como dice el dicho, “lo importante no es lo que sepas, sino a quien conozcas.” La centralidad de eigenvector toma esta idea y la cuantifica en términos matemáticos.
10.1.2 Medidas Basadas en Distancia
10.1.2.1 Centralidad de Cercanía
La medida más común basada en distancia entre nodos es la centralidad de cercanía definida por Freeman (1979) como la distancia geodésica entre un nodo y los demás en una red. Se calcula sumando las distancias geodésicas entre cada nodo y los demás y después invirtiendo el valor para cambiar el índice de una medida de distancia a cercanía (Valente, 2010, p. 85). Es común calcular la centralidad de cercanía como un índice normalizado (con valores de 0 a 1) de la siguiente manera:
\[C_i^{clo} = \frac{N-1}{\sum\limits_{j = 1}^{n}d_{ij}}\]
Donde \(d_{ij}\) es la distancia geodésica entre dos nodos. Adicionalmente, el número máximo teórico de cercanía en cualquier red es \(N-1\), por lo tanto, al dividir el numerador por las distancias sumadas generamos un valor normalizado. El dividir el valor máximo por la suma de las distancias genera un índice donde los valores grandes corresponden a nodos más centrales (Borgatti, Everett, & Johnson, 2018, p. 199).
Calcular esta medida es simple, el grafo 10.4 servirá como ejemplo. Comenzaremos por encontrar los caminos geodésicos entre todos los nodos, presentados en la siguiente matriz de distancias. El siguiente paso consiste en sumar las distancias para cada nodo. Finalmente, dividimos el número máximo teórico de cercanía (\(N-1\)) por la suma de las distancias de cada nodo. Por ejemplo, el nodo A tiene una distancia cumulativa de 15 y el valor teórico máximo de cercanía es 6. Por lo tanto, la cercanía normalizada del nodo A es equivalente a \(\frac{6}{15} = 0.4\).
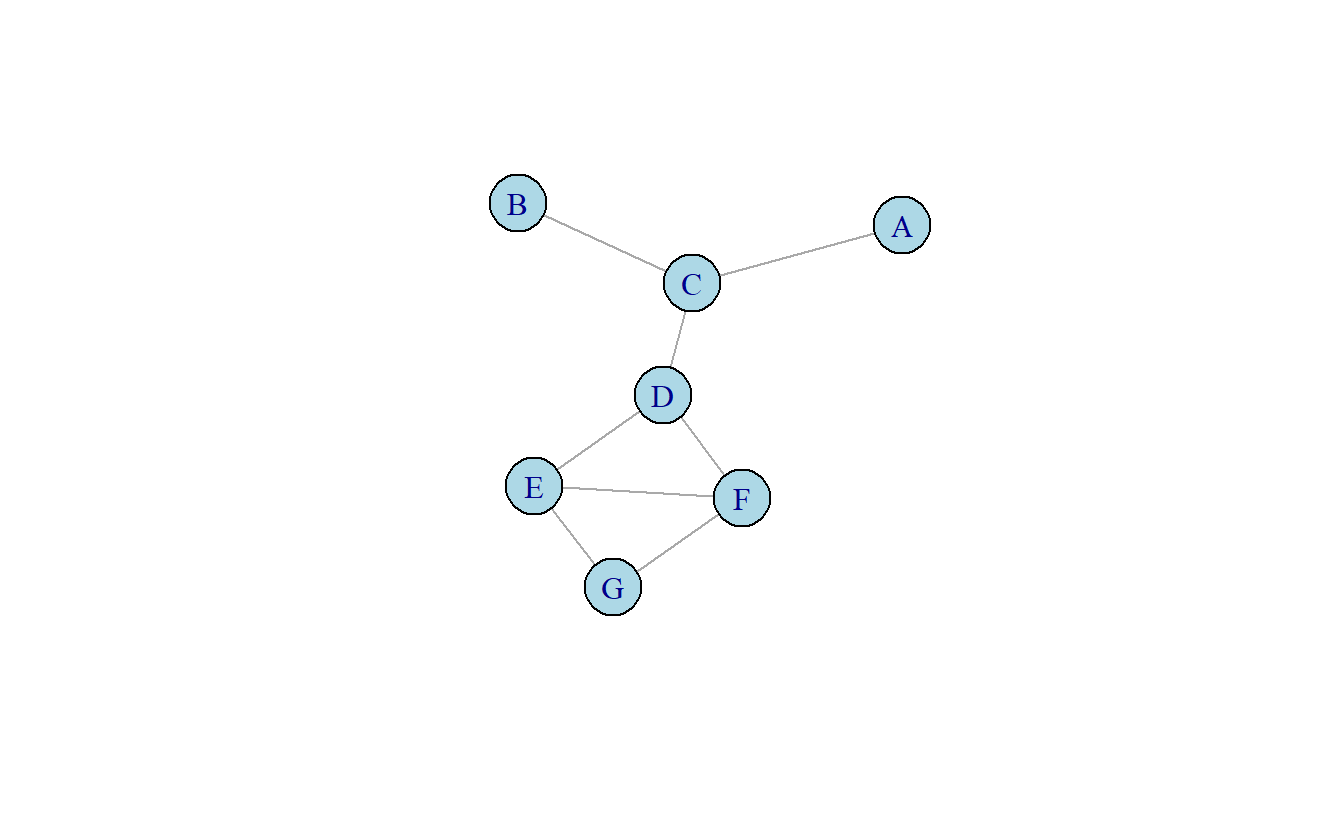
Figura 10.4: Grafo no dirigido
\[ \begin{matrix} & A & B & C & D & E & F & G \\ A & 0 & 2 & 1 & 2 & 3 & 3 & 4 \\ B & 2 & 0 & 1 & 2 & 3 & 3 & 4 \\ C & 1 & 1 & 0 & 1 & 2 & 2 & 3 \\ D & 2 & 2 & 1 & 0 & 1 & 1 & 2 \\ E & 3 & 3 & 2 & 1 & 0 & 1 & 1 \\ F & 3 & 3 & 2 & 1 & 1 & 0 & 1 \\ G & 4 & 4 & 3 & 2 & 1 & 1 & 0 \end{matrix} \quad \begin{matrix} Suma \\ 15 \\ 15 \\ 10 \\ 9 \\ 11 \\ 11 \\ 15 \end{matrix} \qquad \begin{matrix} Cercanía\ Normalizada \\ 0.4 \\ 0.4 \\ 0.6 \\ 0.667 \\ 0.545 \\ 0.545 \\ 0.4 \end{matrix} \tag{10.3} \]
La centralidad de cercanía es una medida intuitiva. Borgatti, Everett, & Johnson (2018) sugieren que en términos de flujo de recursos los nodos más cercanos a menudo reciben materiales, recursos o información rápidamente (Borgatti, Everett, & Johnson, 2018, p. 199). Esto es significativo puesto que los recursos tienden a perder fidelidad a lo largo de distancias de camino largas. Por ejemplo, la información tiende a ser distorsionada conforme cambia de manos en una red o la transferencia de fondos financieros tiende a acumular costos con cada brinco entre nodos. Es por ello que los nodos centrales en términos de cercanía no solo tienden a recibir información, recursos o materiales de manera acelerada, sino también de alta fidelidad.
Antes de concluir la discusión de centralidad de cercanía, es importante entender una de las limitaciones clave de esta medida. Principalmente, el hecho que esta medida no debe ser aplicada al trabajar con grafos con componentes no conexos, por ejemplo, aquel con múltiples componentes. En estas situaciones Cunningham, Everton, & Murphy (2016) sugieren aislar el componente principal antes de calcular la centralidad de cercanía.
10.1.3 Medidas Basadas en Caminos
10.1.3.1 Centralidad de Intermediación
La tercera medida de Freeman (1979) que consideraremos en este capítulo mide la frecuencia con la que un nodo se encuentra en los caminos más cortos conectando a todos los demás en la red. La centralidad de intermediación es comúnmente utilizada por los analistas de redes puesto que identifica actores en posiciones de corretaje claves. Wasserman & Faust (1994) recalcan que interacciones de dos actores no adyacentes pueden depender de aquellos que se encuentran entre esos dos; es decir, los intermediarios que podrían, potencialmente, tener algún control sobre las interacciones entre nodos no adyacentes, o podríamos también decir, tener más influencia interpersonal sobre otros (Wasserman & Faust, 1994).
Calcularemos centralidad de intermediación con la definición formal de Freeman (1979), quien fue uno de los primeros investigadores en cuantificar esta idea. Donde \(g_{jk}\) es el número de caminos más cortos, geodésicos, que unen a dos actores. En un grafo donde los vínculos tienen el mismo peso, es probable que existan múltiples geodésicos entre dos nodos, por ello asumimos que todos los caminos geodésicos tienen la misma probabilidad de ser elegidos, simplemente podemos articular esta idea en términos matemáticos como \(\frac{1}{g_{jk}}\). Puesto que el objetivo es identificar el índice de intermediación de un nodo (\(i\)), \(g_{jk}(n_i)\) representa la porción de los caminos geodésicos que conectan a dos actores \(g_{jk}\) y que contienen al actor \(i\). Freeman define el índice de intermediación de cualquier actor (\(n_i\)) en un grafo como la suma de todas las probabilidades estimadas para todos los pares de nodos en la red sin incluir al actor \(i\) (Wasserman & Faust, 1994):
\[ C_B(n_i) = \sum_{j<k} \frac{g_{jk}(n_i)}{g_{jk}} \]
El índice alcanza su valor máximo cuando el nodo \(n_i\) se encuentra en todas las distancias geodésicas. Por lo tanto, el valor máximo es \(\frac{(n-1)(n-2)}{2}\) que corresponde a el número de actores sin incluir \(n_1\). Podemos utilizar el valor máximo para normalizar el índice a una medida con valores entre 0 y 1, lo cual facilita la comparación con otros índices. Por lo tanto, la centralidad de intermediación normalizada se puede calcular como:
\[ C'_B(n_i) = \frac{\sum_{j<k} \frac{g_{jk}(n_i)}{g_{jk}}}{\frac{(n-1)(n-2)}{2}} \]
Pongamos esta ecuación en práctica. La Figura 10.5 incluye un grafo no dirigido. ¿Qué nodo tendrá la centralidad de intermediación más alta? En este ejemplo le presentamos el cálculo de la centralidad de intermediación de los vértices en el gráfico. Para esta operación el valor máximo es 6 (o \(\frac{(5-1)(5-2)}{2}\)). Los índices presentados han sido normalizados.
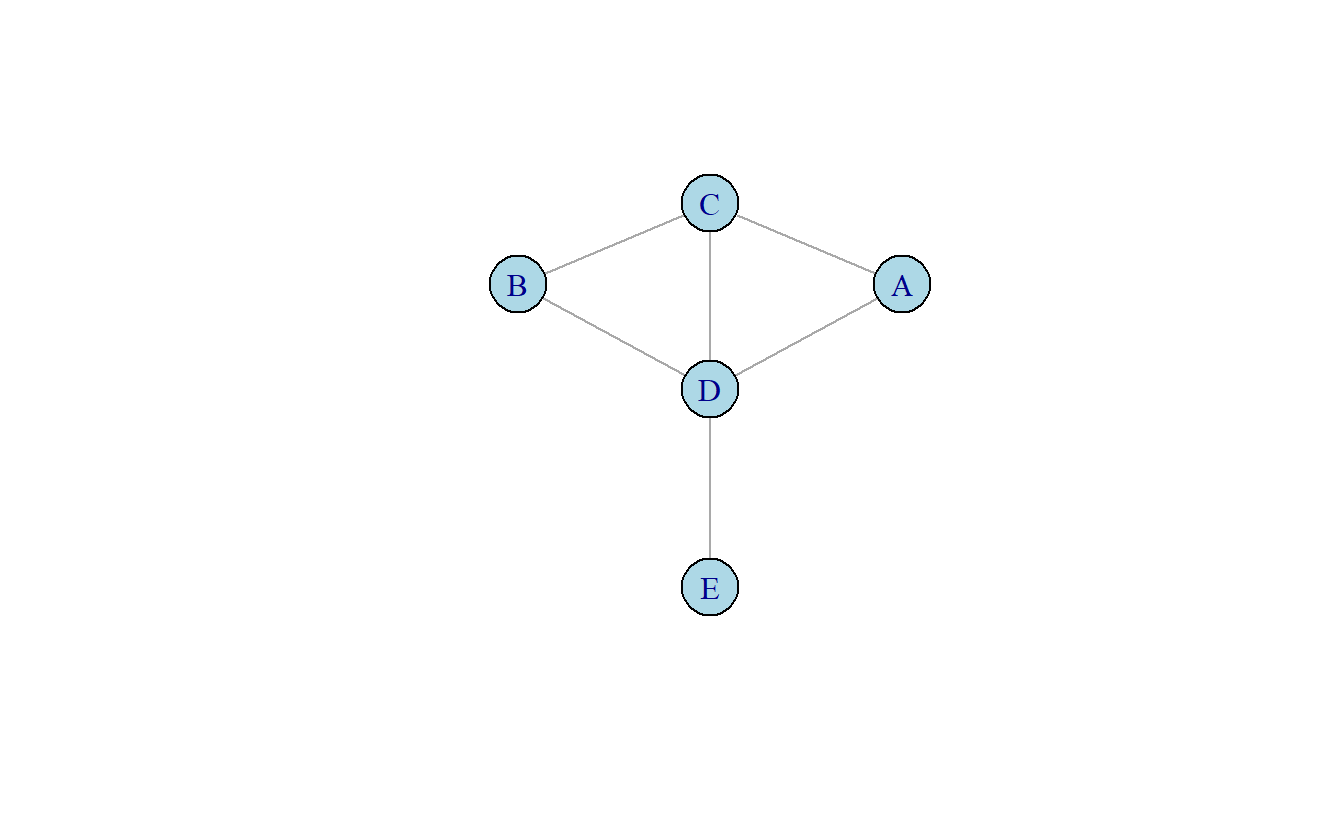
Figura 10.5: Grafo no dirigido simple.
\(Intermediación\ del\ nodo\ A: 0\)
\(Intermediación\ del\ nodo\ B: 0\)
\(Intermediación\ del\ nodo\ C: 0.083\)
\[ Par\ (A, B) = 1/2 \] \[ \frac{0.5}{6} = 0.083 \] \(Intermediación\ del\ nodo\ D: 0.583\)
\[ Par\ (A, B) = 1/2 \]
\[ Par\ (A, E) = 1/1 \\ \]
\[ Par\ (B, E) = 1/1 \\ \]
\[ Par\ (C, E) = 1/1 \\ \]
\[ \frac{0.5+1+1+1}{6} = 0.583 \]
\(Intermediación\ del\ nodo\ E: 0\)
Note que en este índice un nodo puede tener un valor nulo, por ejemplo {A, B, E}. Esto ocurre pues estos nodos no se encuentran en ningún camino geodésico entre otros nodos. El ejemplo más sencillo es el nodo E, que no se encuentra en ningún camino entre nodos pues es un pendiente en la red. Los nodos A y B son redundantes para los demás nodos pues no caen en un camino geodésico, es decir, si E quiere navegar a C la ruta procedería de E a B y luego a C. Otros nodos sirven como posibles intermediadores, por ejemplo C. Este se encuentra en un camino entre A y B. Sin embargo, puesto que existen dos caminos geodésicos entre estos nodos, la porción de caminos entre A y B en la que encontramos a C es solo 0.5. Finalmente, algunos nodos son cruciales para el flujo de la red. Por ejemplo, el nodo D es el punto de acceso a E y se localiza en la mitad de los caminos geodésicos entre A y B.
El proceso demostrado en esta sección es largo y un poco tedioso, sin embargo, los programas de software utilizados por analistas de ARSo producen estos índices con bastante rapidez. Esperamos que pueda ver el valor de esta medida como analista de redes. Simplemente permite identificar nodos cuyo potencial como corredores es mayor en base a su ubicación estructural en una red de nodos. Antes de concluir con esta sección es importante recalcar un punto clave presentado por Cunningham, Everton, & Murphy (2016). Los autores notan que no existe ninguna garantía que dos nodos elijan tomar el camino más corto entre estos en la red (Cunningham, Everton, & Murphy, 2016). En ciertos contextos sociales, el camino más largo puede ser preferible. Por ejemplo, una ruta larga puede ser la única ruta conocida por un par de actores y por lo tanto el camino preferido. Esto no quiere decir que la centralidad de intermediación no tiene valor para el analista de redes, esta medida es útil y comúnmente utilizada pues a menudo aporta nueva información, pero esta debe ser evaluada a par con el contexto de la red.
10.2 Datos Dirigidos: Centralidad y Prestigio
10.2.1 Medidas Basadas en Frecuencia
10.2.1.1 Centralidad de Grado: Entrada y Salida
Retornemos por un segundo a la idea de grados de centralidad, previamente definida en una red no dirigida como el conteo de vínculos de un actor. En un grafo dirigido podemos expandir este concepto para captar la dirección del vínculo adyacente a cada nodo. Específicamente, podemos enfocarnos en los vínculos adyacentes hacia o desde el nodo, que de manera formal llamamos grado de entrada o de salida. Wasserman & Faust (1994) postula que es necesario considerar ambos por separado pues uno cuantifica la tendencia de los nodos a forjar vínculos mientras que el otro la tendencia de recibirlos (Wasserman & Faust, 1994, p. 151).
Considere la Figura 10.6 que incluye un grafo dirigido. La dirección de la flecha indica el nodo que recibe un enlace, del otro lado de la flecha encontramos a aquel nodo que envía dicho arco. La interpretación del grado de entrada o salida depende del contexto del grafo. Por ejemplo, supongamos que los vínculos en la Figura 10.6 representan enlaces de confianza; es decir, cada nodo nomina a otros en la red en quien confía. En esta situación interpretaríamos a un nodo con alto grado de entrada como alguien confiable y un nodo con alto grado de salida como alguien confiado.
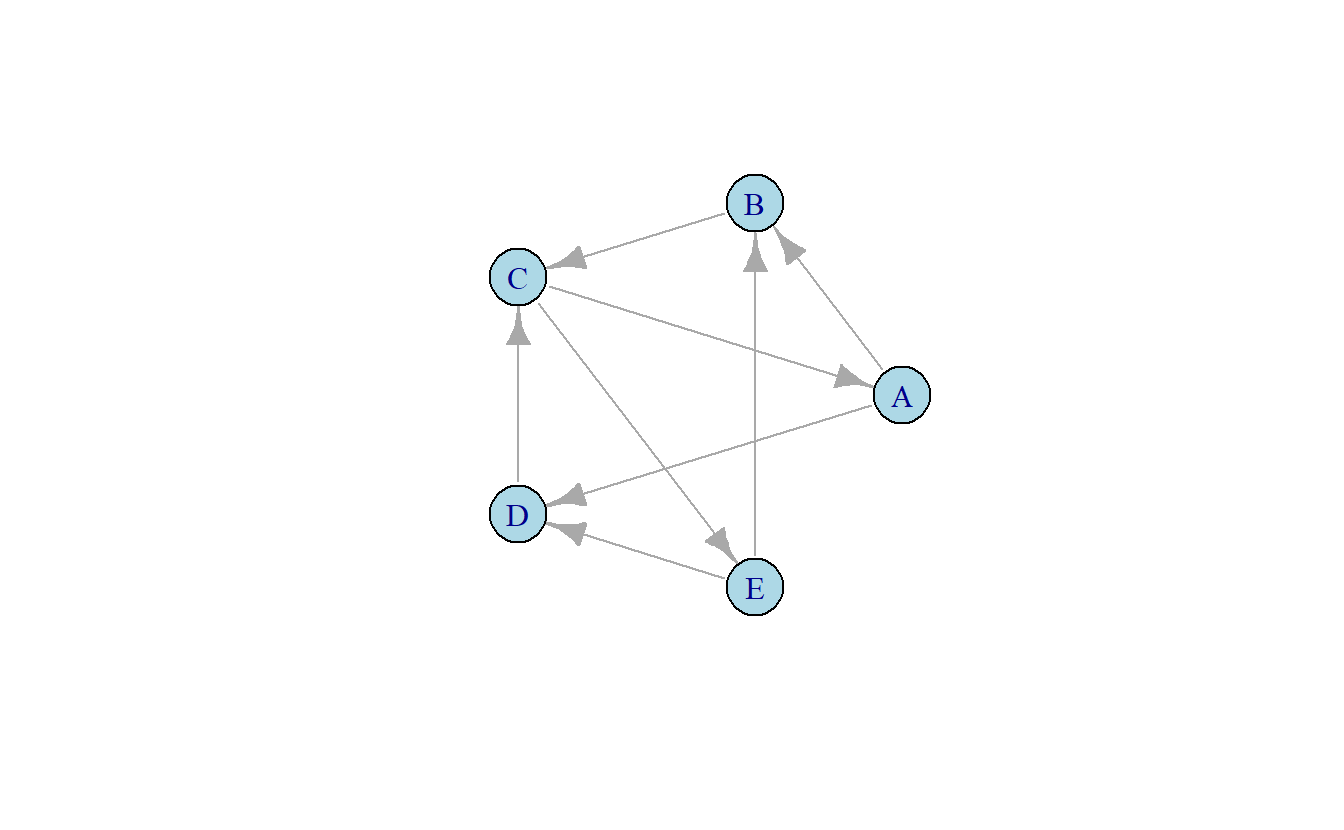
Figura 10.6: Datos dirigidos
Wasserman & Faust (1994) definen el grado de entrada hacia un nodo \(n_i\) como \(d_I(n_i)\), donde el grado de entrada es igual al número de arcos que terminan en \(n_i\) (\(l_k = <n_j, n_i>\)) para todos los arcos (\(l_k\ \epsilon\ L\)) y nodos (\(n_j\ \epsilon\ N\)) en el grafo (\(G(N, L)\)). Similarmente, el grado de salida de un nodo \(d_O(n_i)\) es el número de nodos adyacentes desde \(n_i\). Es decir, todos los enlaces que comienzan en \(n_i\) (\(l_k = <n_i, n_j>\)) para todos los arcos (\(l_k\ \epsilon\ L\)) y nodos (\(n_j\ \epsilon\ N\)) en el grafo (Wasserman & Faust, 1994). En una matriz de adyacencia, la suma de las filas para cada nodo es equivalente a el grado de salida, y los totales de las columnas es igual al grado de entrada. Definimos estas ecuaciones como:
\[ d_O(n_i) = \sum^g_{j=1} x_{ij} = x_{i+}, \]
y
\[ d_O(n_i) = \sum^g_{j=1} x_{ij} = x_{+i}. \]
En términos prácticos el calcular estos valores es simple. La matriz siguiente contiene los datos dirigidos. En este ejemplo, hemos agregados una fila (\(d_I(n_i)\)) y columna (\(d_O(n_i)\)) adicional con los valores de centralidad de entrada y salida. Para calcular dichos índices hemos sumado los valores en la sociomatriz. El sumar las filas, de arriba hacia abajo, resulta en el grado de entrada para cada nodo. Similarmente, el sumar las columnas, de izquierda a derecha produce el grado de salida.
\[ \begin{matrix} & A & B & C & D & E & d_O(n_i) \\ A & 0 & 1 & 0 & 1 & 0 & 2 \\ B & 0 & 0 & 1 & 0 & 0 & 1 \\ C & 1 & 0 & 0 & 1 & 0 & 2 \\ D & 0 & 0 & 1 & 0 & 0 & 1 \\ E & 0 & 1 & 0 & 1 & 0 & 2 \\ \\ d_I(n_i) & 1 & 2 & 2 & 3 & 0 \end{matrix} \tag{10.4} \]
Noté que algunos nodos no reciben ningún enlace, por ejemplo, E tiene un grado de entrada de cero \(d_I(n_E) = 0\). Sin embargo, esta falta de vínculos hacia E no impacta de manera directa el número de enlaces que comienzan con E, \(d_O(n_E) = 2\). El punto clave en interpretar estos índices es el contextualizar las medidas, es decir, hacerse la pregunta como analista: ¿Qué significa un alto grado de entrada o salida con las relaciones presentes?
10.2.1.2 Centros de Actividad y Autoridades
El último algoritmo que exploraremos en esta sección es centros de actividad, o hubs, y autoridades, comúnmente conocido como “hubs and authorities” en inglés o simplemente HITS. Su autor, Kleinberg (1999), originalmente desarrolló esta rutina para clasificar sitios de web. Este algoritmo es similar a la centralidad de eigenvector (Cunningham, Everton, & Murphy, 2016), sin embargo, tiene diferencias cruciales. Fue diseñado para trabajar con datos dirigidos, por lo tanto, genera dos medidas, un índice de centro de actividad y otro de autoridad.
Kleinberg (1999) postula que un centro de actividad sería un nodo enlazado a múltiples autoridades. Es decir, los centros de autoridad actúan como portales que dirigen el tráfico de enlaces hacia nodos eminentes en un tema. Estos últimos son las autoridades, quienes reciben el tráfico de los centros de actividad (Monge & Contractor, 2003). Recuerde que este algoritmo fue diseñado para categorizar sitos de web, es por ello que podemos pensar en centros de actividad como sitios de web a los que acuden las personas buscando información sobre un tema, por ejemplo, Wikipedia. Las autoridades en este contexto serían los sitios de web en la sección de referencias de un tema.
Antes de proceder a calcular los índices, piense ¿En qué contextos sociales piensa usted que un analista de ARSo utilizaría el algoritmo de HITS? Es importante recalcar que, aunque el algoritmo fue diseñado para clasificar sitios de web, tiene múltiples aplicaciones en contextos sociales. Por ejemplo, en una red de comunicación dirigida entre miembros de una organización podemos aislar quienes son los centros de actividad o los nodos que representan las autoridades de la red. En este ejemplo, el localizar un centro de autoridad seria valioso pues, como mencionamos, estos sirven como portales comúnmente utilizados en la red para acceder a autoridades. Similarmente, dependiendo de nuestro objetivo, un nodo en posición de autoridad se encuentra en una posición estructural prestigiosa de la red en cuestión.
En términos prácticos, el calcular los índices para cada nodo de centro de actividad y autoridad es relativamente simple. Observe la red 10.7, los centros de actividad apuntan a las autoridades, esto sucede por la relación mutuamente reforzada donde un buen centro de actividad apunta a muchas buenas autoridades y del otro lado de la moneda una buena autoridad es aquel nodo que recibe múltiples vínculos de buenos centros de actividad (Kleinberg, 1999).
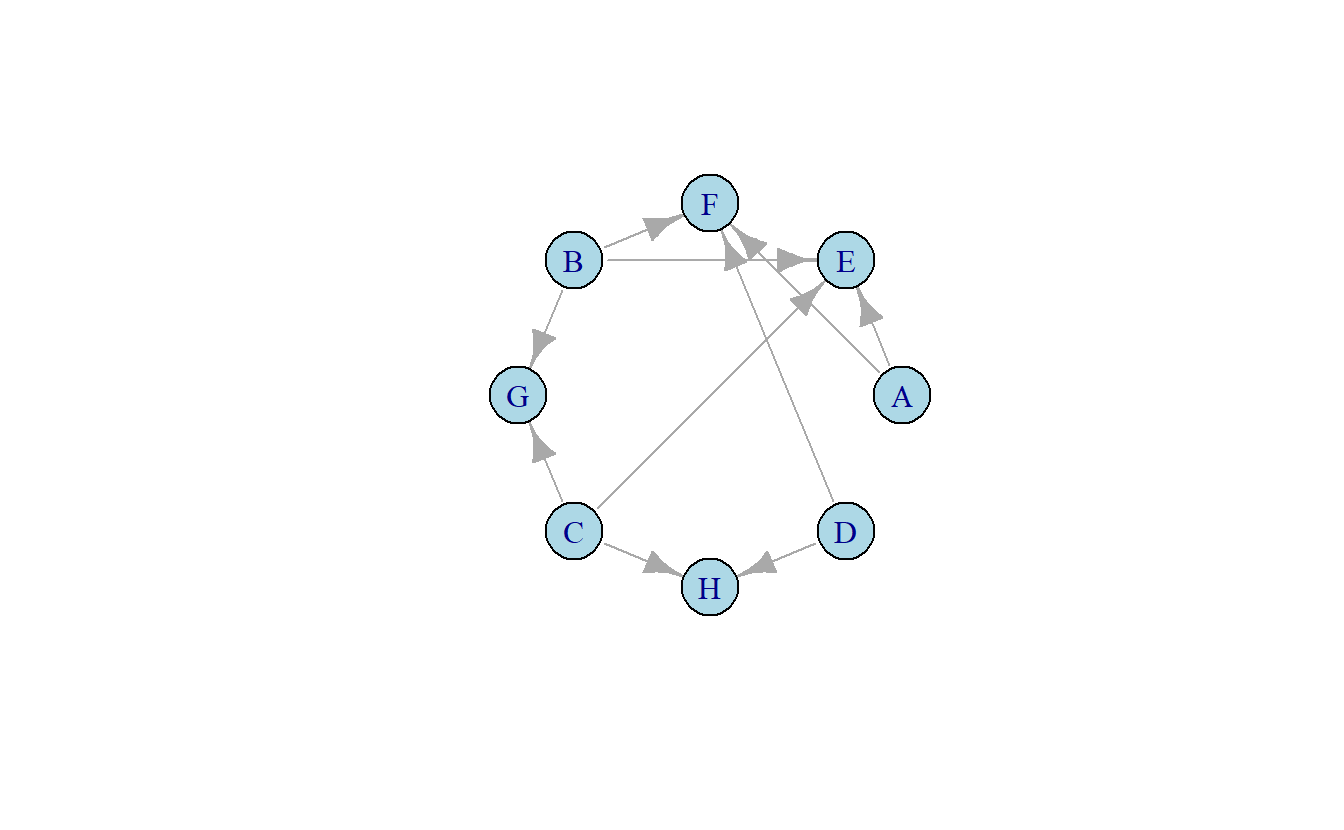
Figura 10.7: Grafo dirigido
Suponga que el nodo \(i\) tiene un índice de autoridad de \(a_i\) y de centro de actividad \(h_i\) donde i es equivalente a \(1:n\). Asuma que la autoridad y centro de actividad inicial de cada nodo \(i\) será \(a_{i}^0\) y \(h_{i}^0\). El método iterativo HITS actualizará los valores iniciales con las siguientes sumas:
\[ a_{i}^k = \sum_{j} h_{j}^{(k-1)} \] \[ h_{i}^k = \sum_{j} a_{j}^{(k-1)} \]
Como proceso iterativo, podemos seleccionar el número de iteraciones \(k\), en este ejemplo utilizaremos \(k=1\). Podemos reescribir las ecuaciones previas como multiplicaciones de matriz:
\[ a^k = A^{T}h_{(k-1)},\ h^k = Aa_{k} \]
Para calcular el primer vector de autoridad \(a^1\), primero debemos transponer la matriz de adyacencia (\(A^T\)) y multiplicarla por el vector inicial de centros de actividad \(h^0\) de valor uno:
\[ \begin{matrix} & A & B & C & D & E & F & G & H \\ A & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ B & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ C & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ D & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ E & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ F & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0 \\ G & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ H & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \\ \end{matrix} \quad \times \quad \begin{matrix} \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{matrix} = \begin{matrix} a^1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 3 \\ 3 \\ 2 \\ 2 \end{matrix} \tag{10.5} \]
Con el vector de autoridad resultante \(a^1\), calcularemos centros de actividad \(h^1\) al multiplicar la matriz de adyacencia \(A\) por el vector de autoridad:
\[ \begin{matrix} & A & B & C & D & E & F & G & H \\ A & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ B & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 0 \\ C & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 1 \\ D & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 \\ E & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ F & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ G & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ H & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{matrix} \quad \times \quad \begin{matrix} \\ 0 \\ 0 \\ 0 \\ 0 \\ 3 \\ 3 \\ 2 \\ 2 \end{matrix} = \begin{matrix} h^1 \\ 6 \\ 8 \\ 7 \\ 5 \\ 0 \\ 0 \\ 0 \\ 0 \end{matrix} \tag{10.6} \]
Para concluir la primera iteración \(k=1\) de este algoritmo, calculamos los eigenvectores normalizados \(||a||\) y \(||v||\) y dividimos cada índice por el valor normalizado. De la siguiente manera:
\[ ||v|| = \sqrt{0^2 + 0^2 + 0^2 + 0^2 + 3^2 + 3^2 + 2^2 + 2^2} = 3.605551 \] \[ ||u|| = \sqrt{6^2 + 8^2 + 7^2 + 5^2 + 0^2 + 0^2 + 0^2 + 0^2} = 13.19091 \] \[ \begin{matrix} & a^1 & h^1 \\ A & \frac{0}{3.6056} = 0 & \frac{6}{13.1909} = 0.4549\\ B & \frac{0}{3.6056} = 0 & \frac{8}{13.1909} = 0.6065\\ C & \frac{0}{3.6056} = 0 & \frac{7}{13.1909} = 0.5307\\ D & \frac{0}{3.6056} = 0 & \frac{5}{13.1909} = 0.379\\ E & \frac{3}{3.6056} = 0.832 & \frac{0}{13.1909} = 0 \\ F & \frac{3}{3.6056} = 0.832 & \frac{0}{13.1909} = 0 \\ G & \frac{2}{3.6056} = 0.5467 & \frac{0}{13.1909} = 0 \\ H & \frac{2}{3.6056} = 0.5467 & \frac{0}{13.1909} = 0 \\ \end{matrix} \tag{10.7} \]
El siguiente ciclo \(k=2\), comenzará utilizando los valores de centros de actividad (\(h^1\)) y autoridades (\(a^1\)) del ciclo previo. El proceso repite una y otra vez dependiente en el número de iteraciones.
Los resultados previos deben corresponder con nuestra intuición, E y F son los nodos más autoritarios, puesto que reciben la mayoría de los enlaces de entrada. Similarmente, B y C son los centros de actividad más activos pues envían la mayor porción de vínculos. El algoritmo HITS nos permite cuantificar que nodos ocupan que posición.
10.3 Ejercicio Práctico
En este ejercicio practicaremos algunas de las medidas de centralidad presentes en Gephi. Para ello necesitara descargar el conjunto de datos titulado: alive_combined_network.gephi.
10.3.1 Centralidad en Gephi
Gephi Archivo > Abrir
Vista general Estadísticas > Grado medio > Ejecutar
- Abra
alive_combined_network.gephi, que puede descargar del sitio que acompaña este manual. Los colores de los nodos de la red reflejan los subgrupos de acuerdo con el algoritmo de Louvain. Gephi implementa un puñado de medidas de centralidad. La medida más común de centralidad es el grado, que en una red no dirigida y binaria es simplemente un recuento del número de vínculos de cada actor (es decir, el número de vecinos). Los vínculos en una red son ponderados cuando los actores comparten múltiples entre sí, por un par de actores puede compartir más de un vínculo, como parentesco, religioso, escolar. Para la centralidad de grado, Gephi ofrece la opción de tomar en cuenta el peso de los vínculos o ignorarlo. Para calcular la centralidad de grado no ponderada, ubique la opción Grado medio en la pestaña Estadísticas y haga clic en Ejecutar. Esto genera un informe, que hemos visto antes, que le presenta la centralidad de grado medio y produce un gráfico que indica la distribución de los valores de grado.
Laboratorio de datos Tabla de datos > Nodos
- En este ejercicio nuestro interés es capturar los puntajes de centralidad de grado de cada actor. Para hacer esto, cambie a la ventana Laboratorio de datos, haga clic en Nodos en la pestaña Tabla de datos, y verá una columna en el extremo derecho con la etiqueta Grado (Figura 10.8). Puede ordenar los actores por grado (ya sea ascendente o descendente) haciendo clic en la etiqueta. Por lo tanto, con un par de clics, puede determinar qué actores son más o menos influentes en términos de grado. Si observa la Figura 10.8, puede ver que Noordin Top ocupa el primer lugar (46), seguido de Suramto (28), Ubeid (27), Abdullah Sunata (25) e Iwan Dharmawan (25). Si desea puede exportar esta tabla y manipular la información en Excel.
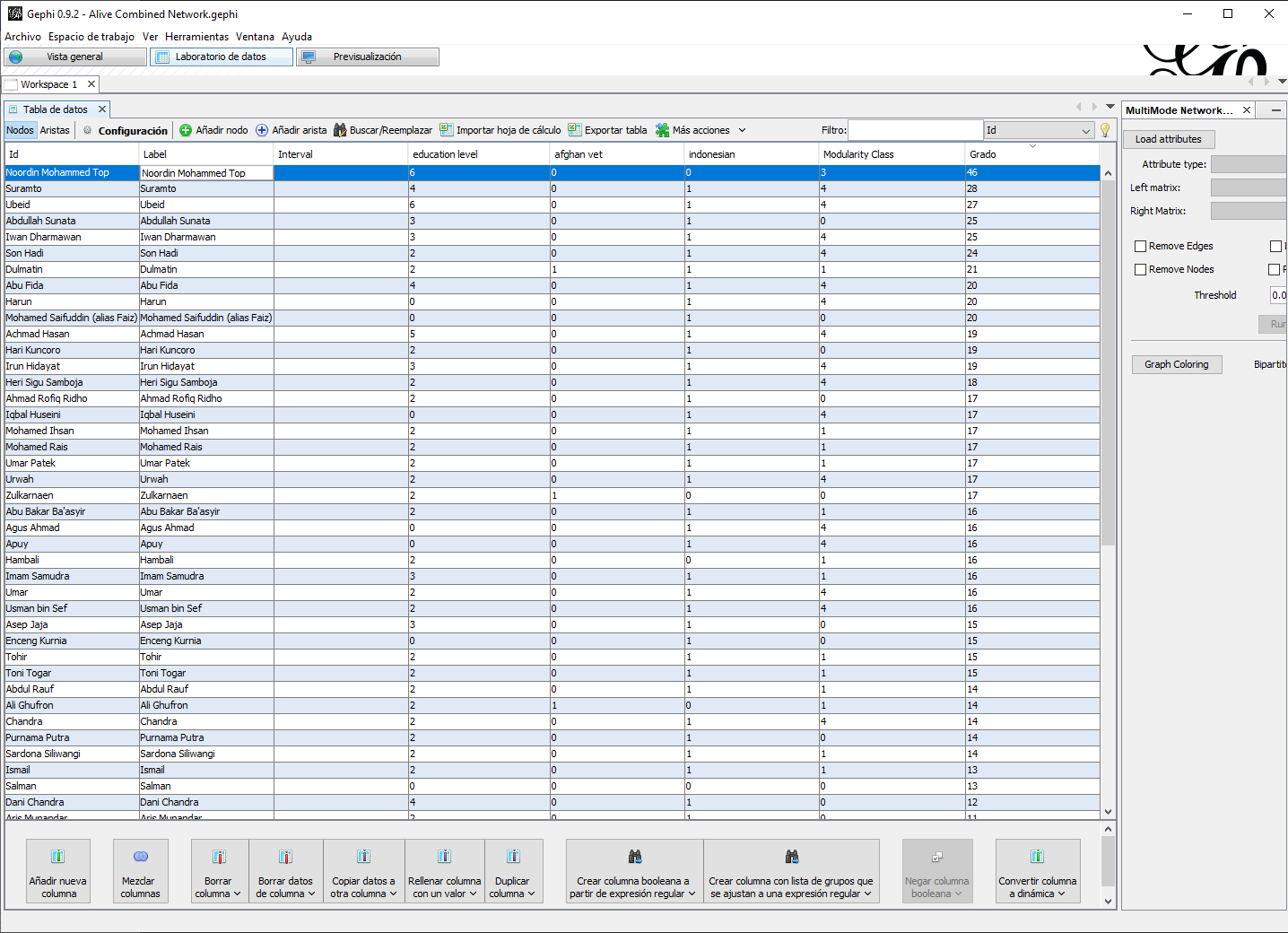
Figura 10.8: Red combinada de nodos vivos, Laboratorio de datos
Apariencia > Nodos Tamaño > Ranking > Aplicar
- Para visualizar la red donde el tamaño del nodo refleja el grado de centralidad, en la pestaña Apariencia, seleccione Nodos, Tamaño y elija Ranking. En el menú desplegable, elija Grado. Haga clic en Aplicar. El gráfico de red resultante debe tener un aspecto similar al de la Figura 10.9.
Figura 10.9: Red combinada de nodos vivos, el tamaño refleja el grado de centralidad
Vista general Estadísticas > Grado medio con pesos > Ejecutar
- Ahora, repita el proceso excepto que esta vez use Grado medio con pesos en lugar de Grado medio. Mire los resultados en la ventana Laboratorio de datos. ¿Qué actor ocupa el puesto más alto? ¿Cuál es su puntuación? ¿Cómo se comparan las clasificaciones con las anteriores que no tenían en cuenta el peso del enlace?
Estadísticas > Longitud media de camino > Ejecutar
- Para obtener la centralidad de cercanía e intermediación en Gephi, podemos usar Longitud media de camino en la pestaña Estadísticas. Al hacer clic en Ejecutar, aparece un cuadro de diálogo (Figura 10.10), que presenta un par de opciones para tratar la red como dirigida o no dirigida (aquí, detecta correctamente que la red no es dirigida). Seleccione la opción para normalizar las centralidades en el rango. La normalización es buena para comparar diferentes medidas. Note que esta opción también calcula la centralidad de excentricidad, que (como indica el cuadro de diálogo) es la distancia desde un nodo en particular hasta el nodo más lejano en la red. Haga clic en Aceptar y Gephi producirá un informe, en el que verá que Gephi calcula dos medidas de proximidad: proximidad (Freeman) y proximidad armónica. Dado que se trata de una red desconectada, utilizaremos la segunda. Como hicimos anteriormente, cambie a la ventana Laboratorio de datos y vea que actores obtienen la puntuación más alta en términos de centralidad de intermediación y cercanía armónica (Harmonic Closeness Centrality).
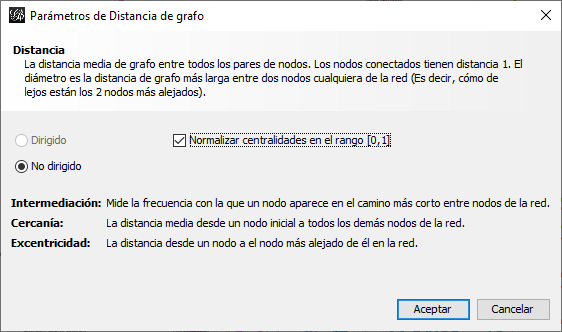
Figura 10.10: Diámetro de red/distancia promedio de camino
Estadísticas > Centralidad del vector propio > Ejecutar
- Finalmente, para estimar la centralidad de eigenvector, usamos la función Centralidad del vector propio de Gephi. En el cuadro de diálogo, indique si la red es dirigida o no y haga clic en Aceptar. Al igual que con las otras funciones de centralidad, genera un informe y almacena las puntuaciones de centralidad para cada actor en la tabla de nodos.